
Attack trees are used in cybersecurity analysis to give an analyst a view of all the ways in which an attack can be carried out. Attack trees can become large, and developing them by hand can be tedious and error-prone. In this paper the automated generation of attack trees is considered. The method proposed is based on a library of attack templates – parameterisable patterns of attacks such as denial of service or eavesdropping – and that also uses an abstract model of the network architecture under attack. A pseudocode implementation of the method is also presented. The example application given is from the automotive domain and using an architecture consisting of linked CAN networks – a network configuration found in virtually every current vehicle.
You have full access to this open access chapter, Download conference paper PDF
Attack trees are a well-known graphical model for capturing and analysing attacks on a system [12]. Their intuitive simplicity and ability to succinctly capture all attacks on a system have made them popular in many domains, including SCADA systems [2], ATM security [4], the analysis of insider attacks [11] and the automotive domain [1]. They give an analyst an overview of all the known ways in which an attack can be carried out, and show how single attack steps combine and build into complex attacks.
Attack trees are directed acyclic graphs with a single end node, which is the goal of the attack. To construct an attack an analyst considers all the steps which would immediately lead to the goal of the attack being realised. These become the subgoals, or intermediate leaves of the tree. Each of these leaves is now considered as a (sub)goal, and the steps that would lead to it’s realisation are identified. The process is recursively repeated until the branches of the tree cannot be further expanded. This process can be time-consuming, especially for large attack trees [4] and several researchers have therefore investigated the automatic generation of the trees [5, 6, 10, 13].
Within the literature, two main approaches to automating the generation or synthesis of attack trees have developed: (i) model transformation and (ii) semantic-based construction. In the model transformation approach, a target system and attackers are modelled using either graphical [6] or formal [13] presentations as input. The desired target of the attackers is identified, and from this the tree root from which the tree construction starts is established. In [6], system models contain actors, processes, items and locations, and connections between these elements to the desired target are utilised to develop the attack tree. Similarly, systems and attackers in [13] are modelled in a process calculus as input. They are first transformed into propositional formulae. Given a target location, these formulae are utilised to construct attack trees by means of backwards-chaining search. While techniques in the model transformation approach are automated, they suffer from lacking a basis for correctness. There is no rigorous relation between generated attack trees and the attacks implicitly implied from input models. In order to fill this gap, [10] proposed ATSyRA, an interactive tool for synthesising attack trees from attack graphs. First, ATSyRA generates all attack paths from the input graphs by model checking. Then, users are required to specify a refinement relation between a set of actions to recursively refine attack paths to eventually construct an attack tree. While ATSyRA establishes the semantic connection between the constructed tree and the input model via attack paths, it is not fully automated. To overcome this shortcoming, [8] introduced an approach to extending an existing attack tree by means of a library of attack trees. The extension is enabled by adding logical preconditions and assertions to tree nodes. Then an attack tree from the library can be attached to a node of the attack tree to be extended if certain relations between the preconditions and assertions are satisfied. To this end, logical reasoning must be employed. Similarly, [5] has proposed a different approach which is based on the formal semantics of attack trees [7]. To this end, the synthesis problem becomes that of generating attack trees from a given semantics, i.e., a set of attack traces. It is reduced to a biclique problem, which is known to be NP-complete, and a heuristic algorithm is suggested for the construction.
In this paper we propose a method for the generation of attack trees based on templates: abstracted and parameterizable known patterns of attack, and represent steps such as spoofing of one node by another, or eavesdropping on traffic between two nodes, which together can be built up into an attack. The method takes as input a description of the architecture of the network that is being attacked and the set of templates.
These networks are modelled by graphs consisting of nodes and connectivity information. Each node represents a component of the network. The network information required includes the access points. These are the nodes within the network that are exposed to attackers outside the network. We present a method that applies each element from the library of attack patterns to the graphical network model in order to form attack trees. We give as well an algorithm for our method. Given a network and a set of templates, the algorithm can generate all possible attacks conforming to the template library.
The contributions in this paper are the template-based method for the generation of attack trees and it’s algorithm, and the automotive example demonstrating the method. The paper proceeds as follows: Sect. 2 begins with an introduction to automotive communication networks and attack trees. In Sect. 3 we give the description of the template-based methodology for generating attack trees, and in Sect. 4 we give the pseudo-code description of the generation algorithm and briefly present the results of our automotive example.
An automotive communication network facilitates the communication between electronic control units (ECUs) within a vehicle. It is usually divided into subnetworks of related ECUs. Depending on the communication requirements of each subnetwork (such as bandwidth, time, etc.), different network types can be employed such as CAN, CANFD, FLEXRAY, LIN, ETHERNET, etc. These networks can be interconnected via Gateway ECUs which will coordinate the traffic between them.
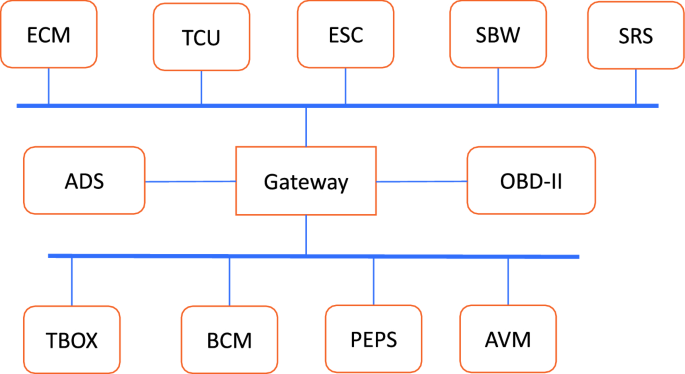
In this paper, we model an automotive communication network as a tuple \((\text , \text , \text , \text )\) where \(\text \) is a finite set of subnetworks, \(\text \) is a finite set of ECUs, \(\text \subseteq \text \) identifies ECUs that are accessible to attackers (such as OBD-II or TBOX), and \(\text :\text \rightarrow \wp (\text )\) is a mapping to determine to which subnetwork an ECU belongs. For example, the network in Fig. 1 is modelled by \(M_f = (\text _f, \text _f, \text _f, \text _f)\) where:
Attack trees contain a goal (the root of the tree), a set of sub-goals, structured using the operators conjunction ( \(\mathbf\) ) and disjunction ( \( \mathbf\) ), and leaf nodes, which represent atomic attacker actions. The \(\mathbf\) nodes are complete when all child nodes are carried out and the \(\mathbf\) nodes are complete when at least one child node is complete.
$$\beginAttack tree semantics have been defined by interpreting the attack tree as a set of series-parallel (SP) graphs [7].
We develop a method to generate attack trees from a network model and a library of attack tree templates. Attack tree templates are building-blocks to assemble an attack tree. Each template from the library represents an attack step within the network which can be applied to different subnetworks and/or ECUs. The adaptability of the attack to various subnetworks and ECUs can be captured by using variables within the template. When the templates are fully instantiated with concrete values from the sets of the network model, it provides a concrete example of an attack on the network.
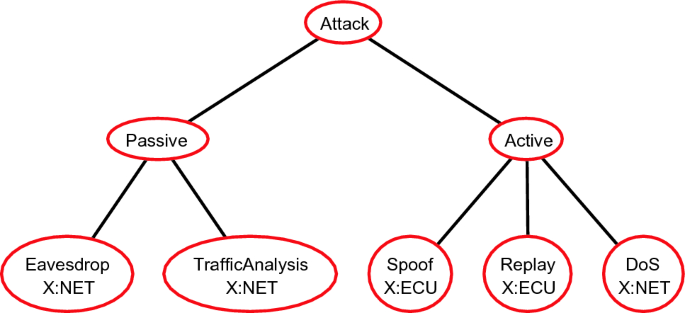
For example, attacks on a communication network can be categorised into two passive or active attacks; eavesdropping and traffic analysis are two examples of passive attacks, while spoofing, replay and DoS (Denial of Service) are active attacks. This is captured in Fig. 2. Variables are used in all the leaves of this template which can be replaced by concrete values. Let us consider the leaf Eavesdrop X:NET. The variables X can be replaced by any value from the component NET of the network model. If we consider the network model \(M_f\) as depicted in Fig. 1, X can be replaced by \(\text _1\) , \(\text _2\) , \(\text _3\) or \(\text _4\) .
The connectivity between ECUs within the network will be represented in attack tree templates using lists. When instantiated, a list of ECUs corresponds to the ability to send data from the first ECU in the list to next one, then the next one, and so on until the data reaches the last ECU in the list. This means consecutive ECUs in the list must belong to the same subnetwork. Gateway ECUs may appear in the list to capture the connectivity between ECUs of different subnetworks. For example, if we consider the model \(M_f\) , a list of ECUs is [ECM, TCU, Gateway, TBOX] where ECM is connected to TCU and TCU to Gateway in \(\text _1\) , and Gateway to TBOX in \(\text _2\) .
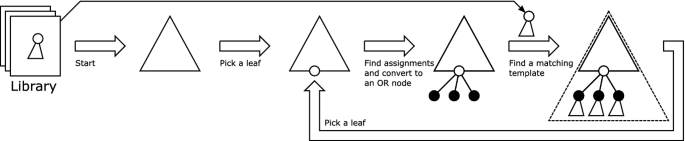
The generation of attack trees starts with a specified template from the library. This template has no closed variables. The generation is carried out recursively. At each recursion, a leaf which may contain open variables is considered for expansion. When there are \(n>0\) assignments for the open variables, this leaf node is converted into an OR node with n children with each child corresponding to one assignment. The assignments are copies of the leaf node where the open variables are replaced by values. Each child is then replaced by a template from the library where the name of the template root matches the name of the child and the parameters of the root can be unified with the parameters of the child. The unification of the parameters will give rise to an assignment of closed variables of the template. The replacement of the child with the template will also replace all closed variables with the values from the assignment. This process is illustrated in Fig. 3. A white circle represents a node with variables while a black one states that its variables have been replaced with values by some assignment.
A special case of assignments is for unassigned lists. An assignment for an unassigned list [X .. Y] is a list of constants from NET and ECU. The start and the end of the list must satisfy any condition for X and Y. For example, consider the network \(M_f\) . An unassigned list [ECM..Y:AP] must be assigned to a list of ECUs from ECM to an ECU that is an access point, i.e, in \(\text _f\) . There are two ECUs that Y can be assigned to: OBD-II and TBOX. Then, one of the list of connected ECUs that [ECM..Y:AP] can be assigned to is [ECM, TCM, Gateway, TBOX] where they are consecutively connected and the last ECU (TBOX) is an access point. Obviously, this is not the only assignment. Two of other candidates to assign this list to are [ECM, Gateway, TBOX] and [ECM, TCM, Gateway, OBD-II].
Assigned lists [X|Y] recursively describe a list with X as the head of the list and Y as the remaining elements, i.e., the tail of the list. [ ] stands for an empty list. An assigned list [X|Y] normally appears at the root of some templates. When it is unified with a list of elements, X will be unified with the head and Y will be unified with the tail. For example, if the list [ECM, TCM, Gateway, TBOX] is unified with [X|Y], then X = ECM and Y = [TCM, Gateway, TBOX].
More formally, nodes in an attack tree template may contain parameters which are made of variables, list terms or constants (i.e., elements of NET and ECU of a network model). Variables can be instantiated with node names. Let N be a set of names for tree nodes, V a set of variables and \(C = \text \cup \text \) a set of constants. The syntax of an attack tree template is defined below:
$$ \begin
where \(X, Y \in V\) , \(n \in N\) and \(c \in C\) .
Informally, an attack tree template is an attack tree in which each node contains a name and possibly a list of parameters. A parameter can be a variable, a constant (node names) or a list of variables and constants. Variables occurring in the root node of an attack tree template are called closed variables. They may reoccur in the descendants of the root. Once root variables are instantiated, their values are propagated down to the descendant nodes correspondingly. In contrast to closed variables, variables in a template that do not appear in its root are called open.
We postulate the following conditions on the occurrence of variables on an attack tree template:
The assignment of values to variables can be restricted with types, by using the condition “: type”. This condition restricts a variable to be instantiated with a constant of type NET, ECU or AP. For example, consider the network in Fig. 1. Given X:NET, X can only be assigned to \(\text _\) , \(\text _\) , \(\text _3\) or \(\text _4\) . Given X:ECU, X can only be assigned to ECM, TCU, Gateway, OBD-II, BCM or TBOX. AP stands for access points OBD-II and TBOX, i.e., places where attackers can have cyber access to the network. Then, X:AP says that X can only be assigned to OBD-II or TBOX. A further restriction can be introduced to the assignment by “/ Y : NET”. Once Y is instantiated with a constant of type NET, “X / Y:NET” states that X can only be assigned to an ECU within the subnetwork Y. For example, “ X / Y:NET” where Y is \(\text _\) means that X can only be assigned to ECM, TCU, or Gateway. Finally, one can require that X is not assigned to an ECU by using the restriction \(\# Z\) where Z is of type ECU. Once Z is instantiated with an ECU, X cannot be assigned to that ECU.
We illustrate our method on an automotive network, depicted in Fig. 4(a). It contains two CAN buses: the powertrain, consisting of three ECUs: ECM (Engine Control Module), TCU (Transmission Control Unit) and GW (the Gateway) and the telematics bus, containing two ECUs: TBox (Telematics Box) accessible to attackers and the same GW, which connects the two buses.
This network is modelled by a tuple \((\text _m, \text _m,\) \(\text _m, \text _f)\) where:
We then consider a library of attack tree templates that focus on how to compromise ECM. The library consists of two templates, depicted in Fig. 4(b) and (c). The template (b) describes a compromise attack on ECM. Essentially, this attack can be realised by starting compromising an ECU to which attackers have access to (Z:AP). Then, the compromise attack can be propagated to the next ECU connected to a compromised one until we reach ECM. This is described by the unassigned list [Z:AP .. ECM]. The template (b) is also specified as the start tree of the generation process. The template (c) describes how compromise attack can be carried out from the first ECU to the last in the list [Z|L]. Note that Z is the head of the list and L is the tail. On Fig. 4(c) the arrow between the edges leading to the two nodes indicates that both nodes must be carried out in order (a \(\mathbf\) node). Not joining the edges in Fig. 4(c) signifies an \(\mathbf\) node, and joining edges with a line (rather than an arrow) signifies that the root node is an \(\mathbf\) node.
This is done by taking control of the ECU Z at the head of the list and then recursively taking control of the rest of the list. Taking control can be done by either re-flashing or gaining root access to Z.
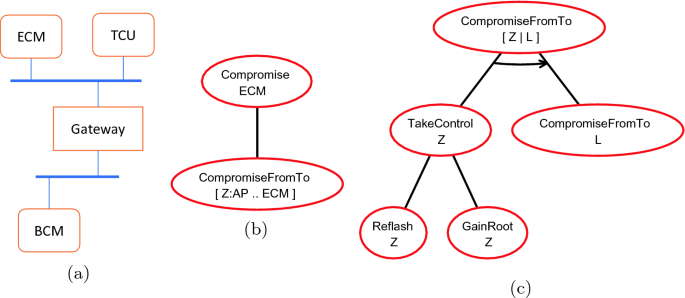
Initially, the construction starts with the template (b) in Fig. 4. The leaf of this expanded tree “CompromiseFromTo [Z:AP .. ECM]” is now considered for further expansion. It has an open parameter which is an unassigned-list. There are two possible assignments for it; one is \([\text , \text , \text ]\) and the other is \([\text ,\text ,\text ,\text ]\) . However, the second list is considered redundant as ECM is directly connected and can communicate with GW without using TCU. This is derived from the nature of CAN bus communication where ECUs on the same bus are directly connected with each other. Therefore, the leaf is appended with one child corresponding to the assignment of [Z:AP .. ECM] to \([\text , \text , \text ]\) . This child is then expanded by the template (c) in Fig. 4. This template is used several times depending on the length of the list. Finally, we obtain the tree Footnote 1 which has height 9 and contains 17 nodes.
We now present the algorithm used to implement our generation method (Algorithm 1.) The inputs are (1) a model of the network structured as in Sect. 2 and (2) a library of attack tree templates and it produces an attack tree as the output.

The algorithm starts with the initial tree InitTree from the input library in line 2. It then loops as long as there is a leaf on the constructed tree and a template, namely subtree, from the library that can be matched. In this loop, all assignments for the variables of the leaf are first computed in line 4. Then for each of the assignments, a unification of subtree and the application of the assignment to the leaf is calculated in line 8. Then the subtree to which the unification is applied is added as a child of the leaf in line 9. Note that the leaf is now converted into an “or” node in line 5. The loop at line 3 will continue until no more leaves and matching templates can be found.
The function apply replaces attack tree template variables with the corresponding values in the input assignment, from the root to the leaves recursively. unify in line 8 is a standard unification procedure. It tries to unify the root of subtree with the leaf to which the considered assignment is applied. It yields a unifier which can be considered as an assignment to the whole subtree.
\(\textsc \) generates Cartesian product of all assignments for the variables and unassigned lists in the input leaf.
We briefly present the experimental result of our implementation on two examples, implemented in Python Footnote 2 and carried out on a PC with a processor Intel Core i5-4590 3.3 GHz with 8GB of memory.
We first rerun the mini example described in Sect. 3.2 which confirms the output tree obtained in Sect. 3.2. Using Python “cProfile” module, the run-time of this experiment is 0.025s and uses 19739 function calls. The second experiment \(^\) is to generate an attack tree for the automotive network \(M_f\) as depicted in Fig. 1. It consists of 4 CAN bus networks with 12 ECUs. The template library contains 21 attack tree templates, including the initial tree as depicted in Fig. 2. In total, the run-time is 0.292s, using 574133 function calls. The generated attack tree Footnote 3 has 3756 nodes and of height 19. An attack example extracted from the tree is an eavesdropping attack carried out at a compromised TCU. Access was gained at the TBOX, then the gateway was compromised followed by the TCU:
GainRoot(TBOX) \(\rightarrow \) Reflash(GW) \(\rightarrow \) Reflash(TCU) \(\rightarrow \) CollectDataFrom(TCU).
In this paper, we have proposed a practical method for identifying all the possible attacks on a known system. We use a library of templates of the atomic attack steps that can be taken against components in the system and give an algorithm for building these into a tree capturing all the attacks. Future steps will include adapting to other types of networks including wireless and ethernet, and also mixed networks which include networks running under different protocols. We also plan to integrate the automated attack tree generation work presented here into work on model-based security test-case generation which currently assumes the existence of the attack tree such as [3].